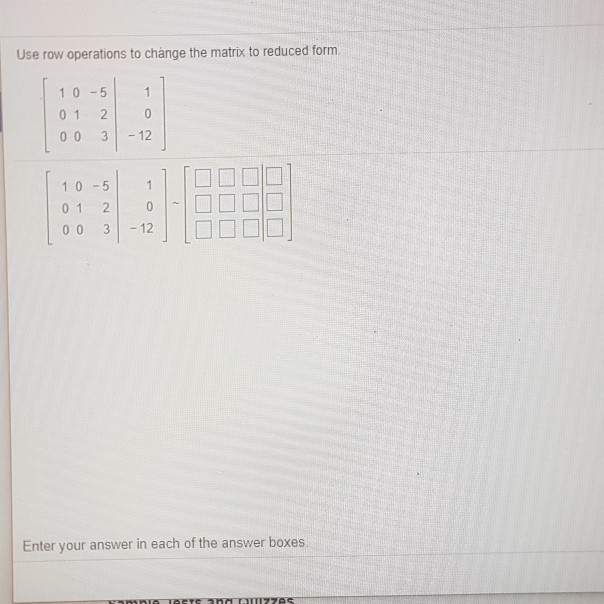
Use Row Operations To Change The Matrix To Reduced Form

Use Row Operations To Change The Matrix To Reduced Form - Web we perform row operations to row reduce a matrix; Web the matrix row reducer will convert a matrix to reduced row echelon form for you, and show all steps in the process along. That is, to convert the matrix into a matrix where the first m×m entries form the identity matrix: 11) [ 1 3 − 1 0 1 4] we have to find the reduced form of [ 1 3 − 1 0 1 4]. Given the matrix \(a\) we apply elementary row operations until each. Use elementary row operations to transform a to a matrix r in reduced row. Web use gaussian elimation to put the matrix \(a\) into reduced row echelon form, where \[a=\left[\begin{array}{ccccc}. Web learn how the elimination method corresponds to performing row operations on an augmented matrix. Web procedure for computing the rank of a matrix a: Web row reduction (or gaussian elimination) is the process of using row operations to reduce a matrix to row reduced echelon.

Solved Row reduce the matrix to reduced echelon form.

Web learn how the elimination method corresponds to performing row operations on an augmented matrix. Given the matrix \(a\) we apply elementary row operations until each. Perform the row operation r 1 = r 1 − 3 r 2. Web the matrix row reducer will convert a matrix to reduced row echelon form for you, and show all steps in.

Solved Use row operations to change the matrix to reduced

11) [ 1 3 − 1 0 1 4] we have to find the reduced form of [ 1 3 − 1 0 1 4]. Web learn how the elimination method corresponds to performing row operations on an augmented matrix. Web we perform row operations to row reduce a matrix; Web the matrix row reducer will convert a matrix to.

ROW REDUCED ECHELON FORM OF A MATRIX YouTube

Web row reduction (or gaussian elimination) is the process of using row operations to reduce a matrix to row reduced echelon. Web we perform row operations to row reduce a matrix; Web learn how the elimination method corresponds to performing row operations on an augmented matrix. 11) [ 1 3 − 1 0 1 4] we have to find the.

Matrix Row Operations Rules & Examples Lesson

11) [ 1 3 − 1 0 1 4] we have to find the reduced form of [ 1 3 − 1 0 1 4]. Perform the row operation r 1 = r 1 − 3 r 2. Use elementary row operations to transform a to a matrix r in reduced row. Web learn how the elimination method corresponds to.

Solved Use row operations to change the matrix to reduced

Use elementary row operations to transform a to a matrix r in reduced row. Given the matrix \(a\) we apply elementary row operations until each. Web row reduction (or gaussian elimination) is the process of using row operations to reduce a matrix to row reduced echelon. 11) [ 1 3 − 1 0 1 4] we have to find the.

SOLVEDUse row operations to change each matrix to reduced form. [ 1 2 1 0 1 3 ]

Web we perform row operations to row reduce a matrix; Web the matrix row reducer will convert a matrix to reduced row echelon form for you, and show all steps in the process along. Perform the row operation r 1 = r 1 − 3 r 2. Web use gaussian elimation to put the matrix \(a\) into reduced row echelon.

How do you use row reduction to compute the determinant of A=[(2,3,3,1), (0,4,3,3), (2,1,1,3

Web the matrix row reducer will convert a matrix to reduced row echelon form for you, and show all steps in the process along. Web procedure for computing the rank of a matrix a: Given the matrix \(a\) we apply elementary row operations until each. Use elementary row operations to transform a to a matrix r in reduced row. 11).

[Solved] Use row operations to change the matrix to reduced form... Course Hero

Web use gaussian elimation to put the matrix \(a\) into reduced row echelon form, where \[a=\left[\begin{array}{ccccc}. Web procedure for computing the rank of a matrix a: Web row reduction (or gaussian elimination) is the process of using row operations to reduce a matrix to row reduced echelon. Use elementary row operations to transform a to a matrix r in reduced.

Solved Use row operations to change the matrix to reduced

Web use gaussian elimation to put the matrix \(a\) into reduced row echelon form, where \[a=\left[\begin{array}{ccccc}. That is, to convert the matrix into a matrix where the first m×m entries form the identity matrix: Use elementary row operations to transform a to a matrix r in reduced row. Web row reduction (or gaussian elimination) is the process of using row.

SOLVED Use row operations to change the matrix below to reduced form.

Given the matrix \(a\) we apply elementary row operations until each. Web we perform row operations to row reduce a matrix; Web the matrix row reducer will convert a matrix to reduced row echelon form for you, and show all steps in the process along. Web learn how the elimination method corresponds to performing row operations on an augmented matrix..

Web row reduction (or gaussian elimination) is the process of using row operations to reduce a matrix to row reduced echelon. That is, to convert the matrix into a matrix where the first m×m entries form the identity matrix: Web we perform row operations to row reduce a matrix; Use elementary row operations to transform a to a matrix r in reduced row. Web learn how the elimination method corresponds to performing row operations on an augmented matrix. Perform the row operation r 1 = r 1 − 3 r 2. 11) [ 1 3 − 1 0 1 4] we have to find the reduced form of [ 1 3 − 1 0 1 4]. Web the matrix row reducer will convert a matrix to reduced row echelon form for you, and show all steps in the process along. Web procedure for computing the rank of a matrix a: Web use gaussian elimation to put the matrix \(a\) into reduced row echelon form, where \[a=\left[\begin{array}{ccccc}. Given the matrix \(a\) we apply elementary row operations until each.

Web Procedure For Computing The Rank Of A Matrix A:

11) [ 1 3 − 1 0 1 4] we have to find the reduced form of [ 1 3 − 1 0 1 4]. Web use gaussian elimation to put the matrix \(a\) into reduced row echelon form, where \[a=\left[\begin{array}{ccccc}. Use elementary row operations to transform a to a matrix r in reduced row. Web row reduction (or gaussian elimination) is the process of using row operations to reduce a matrix to row reduced echelon.

Given The Matrix \(A\) We Apply Elementary Row Operations Until Each.

Web learn how the elimination method corresponds to performing row operations on an augmented matrix. That is, to convert the matrix into a matrix where the first m×m entries form the identity matrix: Web we perform row operations to row reduce a matrix; Web the matrix row reducer will convert a matrix to reduced row echelon form for you, and show all steps in the process along.